Project 3

Face Morphing - Project Spec

  1. Part 1: Defining Correspondences
  2. Part 2: Computing the “Mid-Way” Face
  3. Part 3: The Morph Sequence
  4. Part 4: The “Mean Face” of a Population
  5. Part 5: Caricatures: Extrapolating From the Mean
  6. Bells and Whistles
    1. Morphing music video on a theme
    2. Changing my gender

Part 1: Defining Correspondences

Before any morphing can occur, I had to define corresponding points across the 2 images I wanted to morph. To do this, my friend Elana and I took pictures of each other in the same room with the same expression. I then resized the images so they were the same dimensions, and uploaded them to this tool and manually indicated corresponding points. The points were then exported to a JSON file which was read into my Jupyter notebook I used to code this project.

Next, I computed the midpoint of each corespondence point and performed Delaunay triangulation on the those midpoints. This was done to ensure the triangulation matched both images.

Here is the triangulation for each face.

Rebecca Elana
Rebecca original image Elana original image
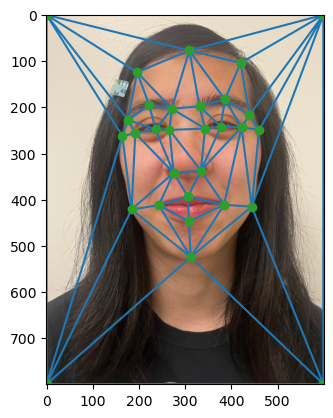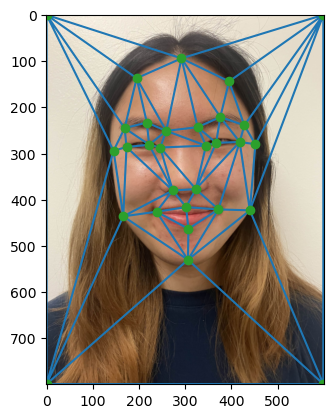Triangulation overlaid over Rebecca original image Triangulation overlaid over Elana original image

Part 2: Computing the “Mid-Way” Face

Next, I used inverse warping to compute the “mid-way” face structure and colors between myself and Elana.

Specifically, for each triangle in the triangulation:

  1. Compute an affine transformation matrix from the source image (either me or Elana) to the average shape
  2. Compute the inverse transformation matrix
  3. For each triangle in the average triangulation:
    1. Get all of the points within the triangle (using skimage.draw.polygon)
    2. Multiply the inverse transformation matrix by all the points in the previous step to get the corresponding points in the source image
    3. Perform nearest neighbor interpolation using scipy.interpolate.griddata using the source image colors to determine the colors for each of the corresponding points within the average triangle
  4. Repeat everything for the second source image

The structure of an affine transformation matrix is like so:

\[\begin{bmatrix} a & b & c \\ d & e & f \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} s_{x_i} \\ s_{y_i} \\ 1 \end{bmatrix} = \begin{bmatrix} d_{x_i} \\ d_{y_i} \\ 1 \end{bmatrix}\]

where \(s_{x_i}, s_{y_i}\) is the source \((x, y)\) pair and \(d_{x_i}, d_{y_i}\) is the destination \((x, y)\) pair. If we are trying to warp a triangle’s vertices, \(i\) is between 1 and 3 (inclusive) since we have 3 coordinate pairs. (However this can be extended to any number of points we want to warp in the same way.)

To find \(a, b, c, d, e, f\), I used numpy.linalg.solve to solve this system of linear equations since we know \(s_x, s_y, d_x, d_y\) for all \(i\):

\[\begin{bmatrix} s_{x_1} & s_{y_1} & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & s_{x_1} & s_{y_1} & 1 \\ s_{x_2} & s_{y_2} & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & s_{x_2} & s_{y_2} & 1 \\ s_{x_3} & s_{y_3} & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & s_{x_3} & s_{y_3} & 1 \end{bmatrix} \begin{bmatrix} a \\ b \\ c \\ d \\ e \\ f \end{bmatrix} = \begin{bmatrix} d_{x_1} \\ d_{y_1} \\ d_{x_2} \\ d_{y_2} \\ d_{x_3} \\ d_{y_3} \end{bmatrix}\]

One challenge I faced while implementing this was realizing that “coordinates” for 2D numpy arrays are actually flipped. When indexing into a numpy array, doing arr[a, b] means getting row a and column b, which means in a typical \((x, y)\) coordinate system, the coordinate would be represented as \((b, a)\) rather than \((a, b)\).

Rebecca Warped to Average Shape Midway Face (Color is the average of the 2 warped images) Elana Warped to Average Shape
Rebecca warped Midway face Elana warped

Part 3: The Morph Sequence

Next I applied the same operation I did in Part 2, except now I also compute intermediate faces (not just the exact middle face) and cross-dissolve 45 frames. This is accomplished by adjusting a warp_frac (controls facial structure) and dissolve_frac (controls colors) that determines how much of the source face versus how much of the destination face is used.

Rebecca to Elana morph sequence

Part 4: The “Mean Face” of a Population

Next, I used this dataset of 40 Danish faces and correspondence points to compute the average neutral Dane face. To do this, I read in each of the images, correspondence files, and warped each face into the average shape (correspondence points). Here are some examples of Danes 5, 7, 12, and 19 warped to the average geometry:

Dane 5 Dane 7
Dane 12 Dane 19

One challenge I faced while reading in the correspondence points was the slightly incorrect documentation of the file format. While the documentation said that the first coordinate was a relative x value and the second coordinate was a relative y value, it was in fact flipped. The first coordinate was a relative row coordinate and the second coordinate was a relative column coordinate, so I didn’t have to do any additional processing to work with the coordinates in numpy arrays like in Part 2.

Then, I stacked the warped faces together and took the average of the colors to get the average neutral Dane face. I also cropped and rescaled the average Dane face so that I could warp myself to the average Dane geometry, and vice versa. You can observe some funny warping behavior because of how my face is not exactly aligned to the face of the average Dane in the dataset (in my picture, my face is vertically higher than the average Dane face).

Average neutral Dane face Rebecca warped to average Dane geometry Average Dane warped to Rebecca geometry
Average neutral Dane face Rebecca to average Dane Average Dane to Rebecca

Part 5: Caricatures: Extrapolating From the Mean

Next I extrapolated from the Dane population mean to create caricatures of myself. Extrapolation works as follows: caricature = scale * (me - avg) + avg where scale > 1.0. This is equivalent to caricature = scale * me + (1 - scale) * avg, which is the same morphing process done in Part 3, where warp_frac is outside the normal range of [0.0, 1.0] and dissolve_frac = 0.0 since we are only changing the geometry of my face.

warp_frac = -0.5 warp_frac = 1.5
Caricature 1 Caricature 2

Bells and Whistles

Morphing music video on a theme

To celebrate the upcoming release of Arcane season 2, I decided to create a morphing music video of the season 2 character posters in the order in which the posters were released: Ekko, Caitlyn, Jinx, and finally Vi. The background music is the instrumental version of the TV show’s title song, Enemy by Imagine Dragons feat. JID.

Here is a link to the video if the embed above doesn’t work. I also cross-posted to the r/arcane subreddit!

Changing my gender

I downloaded the average Asian male face, resized it to match the dimensions of my image, and “changed my gender” by morphing halfway between myself and the average Asian male face (e.g. warp_frac = 0.5 and dissolve_frac = 0.5).

Rebecca Male Rebecca Average Asian Male
Rebecca original image Male Rebecca Average Asian Male